
Comprender el Número f no es algo rápido ni sencillo, ya que hay matemáticas de por medio. Sin embargo, si se explica de forma simple y metódica, no resultará nada complejo, al contrario, nos ayudará a entender muchas otras cosas, como por ejemplo, el tamaño de los lentes. ¿Qué tiene que ver esto con el Número f?, pues lo veremos más adelante.
Hoy en día, el Número f no se utiliza de forma correcta ni precisa, lo cual provoca cierta confusión al momento de entenderlo. Un ejemplo claro es cuando intentamos referirnos a la apertura y decimos “efe cuatro”…
¿nos estaremos refiriendo a “f4”, “F4”, “f/4”, “F/4”, “f=4” o “F=4”?
Probablemente usted haya visto todas estas combinaciones y le aseguro que no aún no tiene claro como debería realmente escribirse. Anote su respuesta mientras tanto y al final de este artículo la podrá verificar.
Lo primero, no debemos confundir F (mayúscula) con f (minúscula).
- F es la Distancia focal
- f es el Número f (que aún no comprendemos)
Conceptos completamente distintos.
A modo de facilitar y simplificar la comprensión en los siguientes apartados:
- Cuando hablemos de Área, nos referiremos al área de apertura.
- Cuando hablemos de diámetro, nos referiremos al diámetro de apertura.
- Cuando hablemos de Luz, nos referiremos a la cantidad de luz que ingresa al sensor.
- El tiempo de exposición no afecta al Número f. Luego, no formará parte del análisis. Lo cual es equivalente a utilizar un tiempo fijo implícito.
- El separador de decimales será el “punto” (por ej. ½ = 0.5), es decir, formato inglés.
Comencemos…
1. Luz vs Área
Si consideramos la Luz como un flujo de rayos luminosos, entonces dicho flujo será directamente proporcional al Área por la cual atraviesa (dinámica de fluidos).
Además, considerando una Distancia focal fija podemos afirmar entonces que:
“Existe una relación proporcional directa entre el Área y la Luz”.
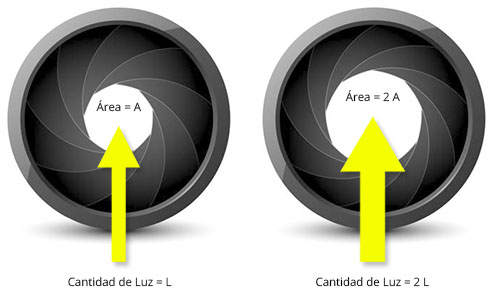
Por lo tanto, si duplicamos el Área, duplicaremos la cantidad de Luz que ingresa al sensor (figura 1).
2. Área vs diámetro
En la figura 2 se representan distintas aperturas en forma de círculo. Las dimensiones que se muestran son de un lente específico, luego, son valores reales tanto de Área (A) como de diámetro (d).
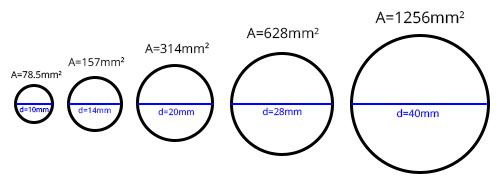
Como podemos ver, las Áreas de los círculos de izquierda a derecha se van duplicando:
78.5mm2 → 157mm2 → 314mm2 → 628mm2 → 1256mm2
Al mismo tiempo, sus diámetros también van aumentando:
10mm → 14mm → 20mm → 28mm → 40mm
Sin embargo, sus diámetros no aumentan el doble, sino que aumentan en un factor √2.
Si es que no comprende esto, la explicación geométrica se detalla a continuación. De lo contrario, puede saltarse directamente al Punto 3.
El área de un círculo es:
A = π r2 (r: radio)
d = 2 r (d: diámetro)
Luego,
A = π (d / 2)2 = π d2 / 4
Despejando d…
d = √ [4 A / π]
Si duplicamos el área, es decir, un nuevo círculo con área A’ y diámetro d’, entonces sabemos que:
A’ = 2 A
d’ = √ [4 A’ / π] = √ [4 (2 A) / π] = √2 · √ [4 A / π] = √2 · d
Entonces,
d’ = √2 d
Es decir, cuando el área se duplica, el diámetro aumenta en un factor √2.
3. Distancia focal vs diámetro
Observe las siguientes figuras:
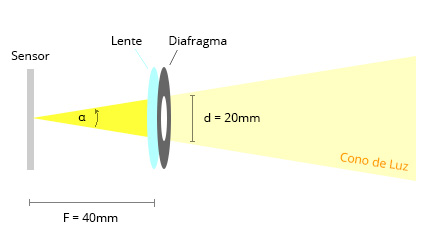
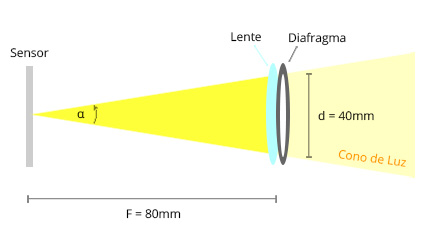
El Cono de Luz que se genera entre el lente y el sensor proporcionará una determinada cantidad de Luz a cada pixel del sensor.
Dado que geométricamente ambos Conos de Luz son equivalentes (figuras 3a y 3b), entonces la cantidad de Luz que ingresará al sensor en ambos casos será la misma.
Debido a que, en ambos casos, tanto la Distancia focal como el diámetro son distintos, entonces podemos afirmar que: La cantidad de Luz no depende únicamente del diámetro sino que además depende de la Distancia focal.
Entonces, lo que determinará la cantidad de Luz será la relación entre la Distancia focal y el diámetro. Esto se conoce como Relación focal y se expresa en forma de cociente:
Relación focal = Distancia focal / diámetro = F / d
Comprobemos su valor en ambas figuras.
Relación focal (figura 3a) = 40mm / 20mm = 2
Relación focal (figura 3b) = 80mm / 40mm = 2
La Relación focal en ambos casos es la misma, igual a 2. Lo cual tiene bastante lógica si se observa la geometría del Cono de Luz (en forma de triángulo), en el cual su altura (que es la Distancia focal) es directamente proporcional a su base (que es el diámetro), y la constante de proporcionalidad es justamente la Relación focal.
Ahora bien, el valor “2” no es, en sí, la cantidad de Luz, ya que como sabemos, la cantidad de Luz depende también del tiempo de exposición. Sin embargo, como estamos considerando un tiempo fijo implícito, el valor “2” si bien, no es la cantidad de Luz, representará una única cantidad de Luz. Y un valor distinto a éste, representará otra cantidad única de Luz.
Ahora, esto se pone interesante…
“El Número f es la Relación focal“.
Luego, llegamos a esta maravillosa fórmula; la esencia misma del Número f:
f = F / d
Es decir,
Número f = Distancia focal / diámetro
4. Número f vs Área
Pregunta al lector:
¿Qué ocurrirá con el Número f si duplicamos el Área?
Como ya sabemos, si duplicamos el Área, el diámetro aumentará en un factor √2, es decir:
Un diámetro d aumentaría a √2 d
Como d = F / f (despejando d de la formula de la Relación Focal)
Luego,
√2 d = √2 F / f
√2 d = F / (f / √2)
Analizando esta última expresión podremos encontrar la respuesta a la pregunta anterior:
“Si duplicamos el Área, el valor de f se reducirá en un factor √2“
Por lo tanto, a mayor Área, menor valor de f.
Dicho de otro modo: A mayor Apertura, menor valor de f. ¿Le parece conocido esto?
Ahora, vuelva usted al ejemplo de la figura 1, y calcule los valores de f para cada uno de los diámetros, sabiendo ahora que la Distancia focal es de 40mm.
Utilice la fórmula f = F / d
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Para el caso de d=20mm:
f = F / d = 40mm / 20mm = 2
…del mismo modo, se calcula el resto de los valores de f.
Finalmente, se obtiene lo siguiente:
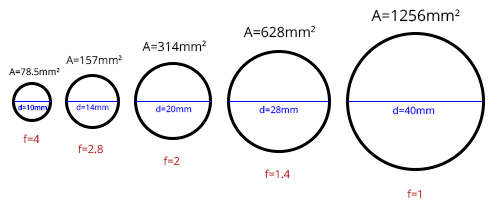
Como podemos observar en la figura 4, de izquierda a derecha:
- El Área se multiplica por 2
- El diámetro se multiplica por √2
- El valor de f se divide por √2
5. Serie del Número f
A continuación, analicemos la secuencia del Número f (figura 5).
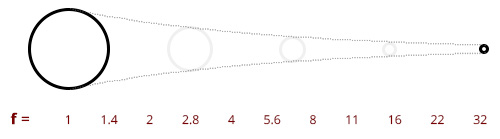
Probablemente usted ya esté familiarizado con estos valores de f, los cuales aumentan a medida que el Área de apertura disminuye. Si observa con atención, el número de izquierda a derecha se va multiplicando por √2.
Esto significa que, dando 2 saltos a la derecha, el valor de f se multiplica por 2 (ya que √2 · √2 = 2). Luego, será fácil memorizarlos.
- Si memoriza el 1, ya tendrá la serie 1, 2, 4, 8, 16, 32…
- Si memoriza el 1.4, ya tendrá la serie 1.4, 2.8, 5.6, 11, 22…
(Los valores 11 y 22 están redondeados y se han acordado de esta manera para su simplificación)
Entonces, a medida que damos 2 saltos hacia la derecha, el valor de f se duplica y el Área se reduce a la cuarta parte. Y viceversa, si realizamos 2 saltos hacia la izquierda, el valor de f se divide por 2 y el Área se cuadruplica… y al mismo tiempo, entrará cuatro veces más Luz.
Pregunta al lector:
Si en su lente tiene seleccionado un valor f=8 y lo cambiase a f=2, ¿cuánta Luz ganaría o perdería?
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Respuesta:
Ganaría 16 veces más Luz, ya que daría 4 saltos hacia la izquierda
(24 = 16)
Como ya vimos, cada salto tiene un factor √2.
Las cámaras actuales cuentan además con saltos intermedios, normalmente ½ salto o ⅓ salto, los cuales son modificables en la configuración de la cámara.
Los valores de f con ½ salto son:
f 1 1.2 1.4 1.7 2 2.4 2.8 3.2 4 4.8 5.6 6.7 8 9.5 11 13 16 19 22 …
Los valores de f con ⅓ salto son:
f 1 1.1 1.2 1.4 1.6 1.8 2 2.2 2.5 2.8 3.2 3.5 4 4.5 5 5.6 6.3 7.1 8 …
Esto justifica por qué existen valores de f como por ejemplo 1.8, en el cual se utiliza una serie de f con ⅓ salto.
6. Nomenclaturas correctas
Cuando hablamos de “F/2.8″, en realidad nos estamos refiriendo a F/f, que es, como ya sabemos, el diámetro de la apertura, y además estamos utilizando un valor de f=2.8. Es por esta razón que cuando usted selecciona el nivel de apertura en su cámara, las opciones son F/1.4, F/2.8, F/5.6, etc., haciendo referencia siempre al diámetro. Al mismo tiempo, F representa la Distancia focal, la cual no tendrá incidencia en la cantidad de Luz, ya que, como vimos anteriormente, un valor 2.8 permitirá ingresar una única cantidad de Luz, independiente de su Distancia focal. Recordemos que f es la Relación focal.
Ahora bien, ¿cuál es la forma correcta para referirse a los valores de apertura?
Respecto al enunciado “F/2.8″, podemos asegurar que:
- F/2.8 es el diámetro
- El valor de f es 2.8
- Es equivalente a “f=2.8”
- Se le puede llamar verbalmente “efe 2.8”, haciendo referencia a f (y no a F)
Una práctica incorrecta, sería confundir F con f, y escribir una en vez de otra.
Volvamos al inicio de este artículo en donde hicimos la primera pregunta. Asumo que tiene anotada su respuesta… veamos si es correcta.
El enunciado decía: Cuando intentamos referirnos a la apertura y decimos “efe cuatro”…
¿nos estaremos refiriendo a “f4”, “F4”, “f/4”, “F/4”, “f=4” o “F=4”?
Según lo aprendido, las respuestas correctas debiesen ser f=4 o F/4 ya que en f=4 hacemos referencia al valor del Número f, y en F/4 hacemos referencia al diámetro de apertura.
Sin embargo, hoy en día, en Internet se encuentra escrito de todas las formas posibles, y son pocas las personas que pueden diferenciar f de F.
¡Qué confuso debiese ser para alguien que no sabe, imaginar que en un apertura “F/4”, F es la Distancia focal!… sí, la misma Distancia focal del lente, y además está dividido por 4, que es el valor del Número f.
En países como EEUU, los valores de apertura se escriben de la forma f/2.8 (con f minúscula). Usando f para referirse a la Distancia focal. Y para referirse al 2.8 (es decir, al Número f) le llaman f-stop, haciendo referencia a que son los valores del Número f cuando nos movemos en un salto (con factor √2). Y al salto mismo le llaman stop.
Finalmente, estamos hablando de lo mismo pero con diferente nomenclatura. Y el concepto f/2.8 o F/2.8 en todos los casos hace siempre referencia al diámetro de la apertura.
Así que, volviendo a la pregunta inicial, todas las respuestas podrían ser válidas. Lo que realmente importa es entender el concepto que hay detrás del -ya no- misterioso Número f.
7. Lentes con gran apertura
Ocurre algo interesante con los lentes de gran apertura, es decir, f bajos. Si volvemos nuevamente a la fórmula d=F/f pero esta vez, analizándola desde otro punto de vista, podremos darnos cuenta que para fabricar lentes con valores de f bajos el tamaño del lente debiese aumentar, sobre todo en los teleobjetivos.
A modo de ejemplo, consideremos un caso real:
El lente Nikon de 400mm F/2.8
Su diámetro de apertura máxima debe ser:
d = 400mm / 2.8 = 143mm
Eso significa que el diámetro físico del lente debe ser mayor a 143mm (que es el diámetro de apertura máxima), lo cual ya es “bastante grande”.
Según sus especificaciones de fábrica, sus dimensiones físicas son:
- diámetro = 160mm
- largo = 358mm
Como podrá imaginar un lente con diámetro 160mm es un lente gigante.
En resumen, no es posible hacer lentes pequeños y portátiles del tipo teleobjetivos con f bajo. Ya que existe una limitación física en el diámetro máximo obligatorio para conseguir dicho valor de f.
Normalmente los teleobjetivos que se usan para deportes son gigantes, y esto se debe a que permiten valores grandes de apertura (f bajos).
Por otro lado, un teleobjetivo con un diámetro físico normal es muy probable que tenga un valor de f=4 o superior, ya que con un valor menor debiese aumentar su tamaño.
Debido a que la gente normalmente prefiere un lente portátil, es que masivamente se fabrican lentes en los cuales se compensa su tamaño con la apertura máxima. Es decir, mientras mayor Distancia focal, mayor f mínimo (menor apertura máxima).
Existe una nominación bien interesante respecto a los lentes que permiten grandes aperturas, normalmente de focal normal o gran angular, a estos lentes se les llaman Lentes Rápidos o Fast Lens, a diferencia de muchos teleobjetivos que por temas de limitación de tamaño los fabricantes se ven obligados a reducir su apertura máxima, a estos últimos se les llama Lentes Lentos o Slow Lens. El Lente Rápido no es más que un concepto que se relaciona con la alta velocidad de obturación que permite alcanzar dicho lente.
Finalizando este artículo…
No olvidar que Número f es un valor sin unidad que se relaciona de forma directa con la cantidad de Luz que llega al sensor; que no depende ni de la Distancia focal, ni del diámetro, ni del Área. Así que, a partir de ahora, lo podemos poner a trabajar con su gran amigo: el tiempo de exposición, que son los únicos que determinarán la cantidad de Luz que ingresará al sensor.
¿Le gustaría aprender más?
► Curso de Nitidez y Enfoque





























Esta es la primera aclaración sobre el numero f que leo que sea muy bien explicada. Muchas gracias!
Excelente explicación. Gracias!!
Me alegro que te haya gustado 😉
Saludos.
Muy buen artículo, 100% recomendado
Muchas gracias David!
Muy buena y dudactica tu explicación. Justo lo que estaba buscando. Un millón de gracias. Solo tengo una seria difivultad por que no logro ver como llegas a esta conclusión de lo que ocurre al número f cuando duplicamos el área y por lo tanto el diámetro con el facto raíz de dos.
√2 d = √2 F / f
√2 d = F / (f / √2)
Cómo llega esa raíz de dos a la variable f si antes está multiplicando toda la expresion F/f
Hola Héctor,
Haz el proceso inverso, parte de √2 d = F / (f / √2)
y verás que llegarás a √2 d = √2 F / f
La expresión √2 F / f
es lo mismo que: √2 * F / f
y es lo mismo que: √2 (F / f)
Espero haberte respondido.
Me alegro que hayas disfrutado el artículo.
Muchisimas gracias por tu respuesta Felipe. Muy amable de tu parte. Y reitero que este contenido fue lo más didáctico y claro que he encontrado. Y mira que estuve buscando y leyendo. Gracias por tu tiempo.
Excelente artículo, super claro y es una información que todos debiéramos leer .
Qué bueno que lo hayas disfrutado.
Saludos.
Excelente artículo. Me quedó clarísimo,
Saludos
Gracias Rodrigo!